Ellipsa

En geometria, l’ellipsa (en grèc ancian: ἔλλειψις, significant «mancança») es una corba plan barrat apertenent a la familha de las còniques que pòt s'obténer es a dire coma seccion d'un con circular amb un plan; o la figura formada per l’ombra d'un disc sus una superfícia plana.
En matematicas, e pus particularament en geometria euclidiana de dimension tres, una ellipsa es una corba plana sarrada obtenguda coma projeccion d'un cercle sus un plan - pron que la direccion de la projeccion siá pas parallèla au plan dau cercle - , o coma interseccion d’un còn drech amb un plan; fau alora que lo plan siá pas trop «clinat», valent a dire que l'angle entre la normala au plan e l'axe dau còn siá inferior au complementari de l'angle dau còn[1]. Lo cercle es una ellipsa particulara.
En geometria euclidiana plana, l'ellipsa es lo luòc dei ponchs que la soma de sei distàncias en dos ponchs fixes, dichs fòcus, es constanta (sa construccion per lo metòde dau jardinier es fòrça simpla).
S'atròba tanben, en premiera aproximacion[2], d'ellipsas dins lei trajectòrias dei còrs celèsts (planetas, cometas o satellits artificiaus) en orbita a l'entorn d'una estela o d’una autra planeta. Ansin, l'orbita de la Tèrra es una ellipsa que lo Soleu n'es un fòcus.
Definicions geometricas
[modificar | Modificar lo còdi]Directritz e fòcus
[modificar | Modificar lo còdi]
Lo quadre es un plan afin euclidian . Sián dins aqueu plan: una drecha, e un ponch qu'apartèn pas a ; estent un nombre reau de l'interval , se sòna ellipsa de drecha directritz , de fòcus e d'excentricitat l'ensemble dei ponchs dau plan taus que:
onte es la distància dau ponch au ponch e es aquela de a la drecha .
Notem la projeccion ortogonala de sus . Es clar que la drecha es un axe de simetria de l'ellipsa, dich axe focau o axe major.
Definicion bifocala de l'ellipsa
[modificar | Modificar lo còdi]
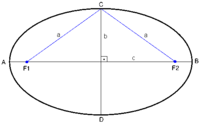
Sián e dos ponchs distints dau plan, e a un reau tau que
Se sòna ellipsa de fòcus e l'ensemble dei ponchs dau plan que verifican la proprietat seguenta:
D'elements de simetria de l'ellipsa (axes de simetria, centre de simetria) apareisson immediatament:
- la drecha ; es l'axe focau o axe major ja mencionat
- la mediatritz dau segment ; es l'axe dich menor de l'ellipsa
- lo mitan dau segment ; es sonat centre de l'ellipsa
Lei ponchs d'interseccion (A, B) de l'ellipsa amb son axe major son dichs vertèx principaus; lei ponchs d'interseccion (C, D) de l'ellipsa amb son axe menor son dichs vertèx segondaris. Alora:
- : se ditz[3] que 2a es la longor de l'axe major
Se definís:
- : se ditz que 2b es la longor de l'axe menor
Coma:
se'n dedutz:
e resulta dau teorèma de Pitagòras que
Imatge d'un cercle per una afinitat
[modificar | Modificar lo còdi]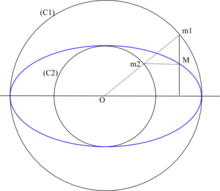
Sián un cercle de centre e de rai , un cercle de centre e de rai () e una drecha passant per . Se sòna ellipsa de centre , de semiaxe major e de semiaxe menor l'imatge dau cercle per l'afinitat d'axe , de direccion perpendiculara a e de repòrt /.
Per construire lo ponch de l'ellipsa, imatge dau ponch dau grand cercle, se construtz lo ponch dau cercle situat sus . Se traça per la perpendiculara a e per la parallèla a . Lei drechas se copan en . D'efiech, se es la projeccion ortogonala de sus , alora, d'après lo teorèma de Talès,
Seccion conica
[modificar | Modificar lo còdi]
L’ellipsa es una corba plana de la familha dei conicas. S'obtèn coma l’interseccion d'un plan amb un còn de revolucion quand aqueu plan travèrsa lo còn de part en part. Lo cercle apareis coma una ellipsa particulara (plan de copa perpendicular).
Entre lei conicas, leis ellipsas se caracterizan per una excentricitat estrictament compresa entre 0 e 1.
Proprietats geometricas
[modificar | Modificar lo còdi]Elements de simetria
[modificar | Modificar lo còdi]S'es ja mencionat
- l'« axe focau », o « axe major », passant per lo fòcus e perpendicular a la directritz, axe de simetria de l'ellipsa
- l'«axe menor», perpendicular a l'axe major, autre axe de simetria
- lo «centre», interseccion deis axes major e menor, centre de simetria de l'ellipsa
Tangenta e bisectritz
[modificar | Modificar lo còdi]
Siá una ellipsa que sei fòcus son e . En un ponch d'aquela ellipsa, se considèra la bisectritz dau sector angular . Alora, aquela bisectritz es perpendiculara a la tangenta en (se ditz qu'es normala en M a l'ellipsa).
Aquela proprietat s'utiliza en optica geometrica dins lei miraus elliptics: un rai luminós que passa per un dei fòcus, quand es reflectit, passa per l'autre fòcus. Ansin, se se plaça una ampola a un fòcus d'un mirau elliptic, lo fais luminós se concentra sus l'autre fòcus.
Aiçò explica tanben lo fach que lei sons se propagan fòrça ben d'un quai a l'autre dau mètro parisenc. D'efiech, la màger part deis estacions an una forma elliptica. Se la fònt d'un son s'atròba en un dei fòcus, totei lei sons reflectits convergiràn vèrs l'autre fòcus (sus l'autre quai). Aquela proprietat de l'ellipsa s'explica en se servent de la tangenta en un ponch de l'ellipsa: d'aqueu biais, un son o un rai luminós emés d'un dei fòcus serà reflectit sus l'autre fòcus. Aquela proprietat s'utiliza dins la concepcion de cèrts instruments d'optica. Es de segur presenta dins una galariá amb ressòn, valent a dire dins una pèça que son plafon, per sa forma elliptica, fa qu'una persona que chuchoteja en un dei fòcus s'ause a l'autre fòcus. La rotonda dau Capital Building a Washington e lo Mormon Tabernacle a Salt Lake City son d'exemples d'aquela mena de galariás[4].
Relacions entre lei grandors
[modificar | Modificar lo còdi]
Lei grandors (geometricas o numericas) d'una ellipsa son
- la longor dau grand rai (o semiaxe major), generalament notada a ;
- la longor dau pichon rai (o semiaxe menor), generalament notada b ;
- la distància separant lo centre de l'ellipsa e un dei fòcus, generalament notada c ;
- la distància separant un fòcus F de sa directritz (d) associada, generalament notada h ;
- l'excentricitat de l'ellipsa (estrictament compresa entre 0 e 1), generalament notada e ;
- lo paramètre de l'ellipsa, generalament noté p.
Existisson de relacions entre aquelei grandors:
- se se definís l'ellipsa per son excentricitat e la distància entre lo fòcus F e la directritz (d), alora
- ;
- ;
- ;
- ;
- se se definís l'ellipsa per sei rais e
- onte ;
- ;
- ;
- ;
- enfin, quand se conois lo grand rai e l'excentricitat :
- .
Eqüacions caracteristicas
[modificar | Modificar lo còdi]Eqüacion cartesiana
[modificar | Modificar lo còdi]Eqüacion reducha
[modificar | Modificar lo còdi]Dins lo sistèma de coordenadas definit per l'axe major e l'axe menor de l'ellipsa, son eqüacion es (se l'axe focau es aqueu deis abscissas):
(se l'axe focau es aqueu deis ordenadas, se deu escambiar a e b).
Eqüacion generala
[modificar | Modificar lo còdi]Dins un sistèma quin que siá de coordenadas cartesianas, tota conica, e en particular tota ellipsa, a una eqüacion de la forma:
- (onte lei reaus A, B, C son pas totei nuls)
Una condicion necessària e sufisenta per qu'una tala eqüacion siá la d'una ellipsa es que:
- (leis expressions entre lei barras verticalas son de determinants)
autrament dich:
Se B = 0, leis axes de l'ellipsa son parallèls ais axes de coordenadas, e reciprocament.
Es classic que se l'ensemble definit per l'eqüacion
es una ellipsa, alora , e que reciprocament, se , alora l'ensemble definit per aquela eqüacion (çò es: l'ensemble dei ponchs dau plan que sei coordenadas (x, y) la complisson) es una ellipsa, o un singleton, o es vuege.
Se supausa desenant que:
Alora A ≠ 0. Se pòt definir:
L'eqüacion (1) es equivalenta a:
o
Se remarca que:
- (d'après l'ipotèsi (2))
Per aleujar lei notacions, se pausa:
Inversament:
Amb aquelei notacions, l'eqüacion (5) es equivalenta a:
o
o
e finalament, d'après (6), l'eqüacion (1) equivau a la seguenta:
onte
- .
D'après (3) e un calcul que se detalharà pas aicí:
- .
Se remarca alora que, segon l'ipotèsi (2), S a meteis signe que lo produch seguent:
Se conclutz ara la demostracion. D'après (10) (qu'es ren qu'una reescritura de (1)):
- se T < 0 (doncas S < 0), l'ensemble definit per l'eqüacion (1) es vuege (la soma dei carrats de nombres reaus es necessariament positiva o nulla)
- se T = 0 (doncas S = 0) l'ensemble definit per l'eqüacion (1) es constituit d'un element unic (se la soma dei carrats de nombres reaus es nulla, cadun d'aquelei reaus es nul, çò qu'aicí determina completament x e y)
- se T > 0 (doncas S > 0), l'ensemble definit per l'eqüacion (1) es constituit de mai d'un element: es una ellipsa.
dins lo sistèma de coordenadas definit per l'axe major e l'axe menor; lo reau t es l'anomalia excentrica dau ponch M de l'ellipsa.
Eqüacion polara
[modificar | Modificar lo còdi]dins lo sistèma de coordenadas definit per lo fòcus e l'axe focau.
o
dins lo sistèma de coordenadas definit per lo centre e l'axe focau.
Circonferéncia
[modificar | Modificar lo còdi]La circonferéncia d'una ellipsa es , onte es una integrala elliptica complèta de segonda espècia.
Sota forma d'una seria, s'escriu:
Una bòna aproximacion es balhada per una formula de Ramanujan:
que se pòt tanben escriure:
onte es la semilongor de l'axe major e la semilongor de l'axe menor.
Pus generalament, la longor de l'arc en foncion de l'angle sostendut es balhada per una integrala elliptica incomplèta de segonda espècia. La foncion recipròca, l'angle sostendut en foncion de la longor de l'arc, es balhada per lei foncions ellipticas.
Aira dau domeni interior an una ellipsa
[modificar | Modificar lo còdi]L'aira dau domeni interior an una ellipsa que sei semiaxes an per longors respectivas a e b es:
Se remarca que per , se retròba l'aira dau domeni interior an un cercle de rai a (o disc de rai a).
Existisson divèrsei manieras de calcular l'aira dau domeni interior an una ellipsa. Òm se pòt plaçar dins lo sistèma de coordenadas cartesianas onte l'eqüacion de l'ellipsa s'escriu:
Amb lei simetrias establidas supra, sufís de calcular per exemple l'aira de la porcion dau domeni situada dins lo quart superior drech dau plan (definit segon aqueu sistèma de coordenadas). L'eqüacion de l'arc d'ellipsa correspondent es:
per dins . D'onte l'aira dau quart superior drech:
- (la darriera escritura s'obtèn amb lo cambiament de variabla de sus )
Rèsta de linearizar per acabar aqueu calcul:
Enfin, l'aira entiera dau domeni interior a l'ellipsa es:
Dessenhar una ellipsa: lo metòde dau jardinier
[modificar | Modificar lo còdi]
Segon la definicion bifocala, lei ponchs de l'ellipsa son lei ponchs dau plan taus que la soma de sei distàncias ai dos fòcus e es constanta. Ansin, per traçar l'ellipsa, se planta dos piquets dins lo sòu (lei dos fòcus), se pren una còrda non elastica (que sa longor es la soma constanta) e se n'estaca leis extremitats ai piquets; se mantèn la còrda tesada per mejan d'una cavilha (per plantar): la cavilha dessenha una ellipsa.
An aquela tecnica, se li ditz « l'ellipsa dau jardinier ».
L'ellipsa en mecanica celèsta
[modificar | Modificar lo còdi]En mecanica celèsta, un còrs somés a l'atraccion gravitacionala d'un autre e que vira a son entorn, descriu una orbita elliptica. Un dei fòcus de l'ellipsa coïncidís amb lo còrs atractor. L'excentricitat de la trajectòria depend dei condicions inicialas. Cf. l'article subre lei lèis de Kepler.
Vejatz tanben
[modificar | Modificar lo còdi]Liames intèrnes
[modificar | Modificar lo còdi]Nòtas e referéncias
[modificar | Modificar lo còdi]- ↑ Angle entre l'axe dau còn e una directritz.
- ↑ Vejatz problèma dei dos còrs e problèma dei N còrs.
- ↑ Terminologia usuala, mai abusiva, que l'axe major es la drecha (A, B) e non pas lo segment [A, B].
- ↑ Swokowski. Analyse. Traduccion: Micheline Citta. 5ena edicion.





![{\displaystyle ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f6a83a50a400fb17f0c9abe6e674c6526a7b0e1)











![{\displaystyle [F_{1}\,F_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9f6e4b319b145172a2063b6f0dd8976e5acac80)















![{\displaystyle [Om_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bb87c0273b1fd42f988b1dfb9d5c082dee8c199)









































![{\displaystyle c=2\pi a\left[{1-\left({1 \over 2}\right)^{2}e^{2}-\left({1\cdot 3 \over 2\cdot 4}\right)^{2}{e^{4} \over 3}-\left({1\cdot 3\cdot 5 \over 2\cdot 4\cdot 6}\right)^{2}{e^{6} \over 5}-\cdots }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e04c08431ae3402d44953a2b0098cb222f3416ac)
![{\displaystyle c\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da7031ad76039c78a15fd2fa7e876534e0729812)
![{\displaystyle c\approx \pi a\left[3(1+{\sqrt {1-e^{2}}})-{\sqrt {(3+{\sqrt {1-e^{2}}})(1+3{\sqrt {1-e^{2}}})}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2530f15f4ee4e0ecfe7df7baf53451dffb1a85e0)





![{\displaystyle [0,\,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ba1694bdf122a23e83606eee0887c887f477ed)


![{\displaystyle [0,\,\pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e17892438792de278539dbf734afa7f6cbb3df49)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)



