Ensemble
Lo concèpte d'ensemble (var. ensems, al plural ensemses o ensems)[1] es fondamentau en matematica modèrna. La teoria deis ensembles foguèt introducha a la fin dau sègle xix per lo matematician alemand Georg Cantor.
Intuitivament, lo tèrme d'ensemble designa una colleccion d'objèctes sonats elements de l'ensemble. Lo concèpte d'ensemble se caracteriza essencialament per lei proprietats seguentas :
- se pòt dire sens ambigüitat s'un objècte apartèn o non a un ensemble donat, autrament dich se n'es o se n'es pas un element ;
- leis elements d'un ensemble lo determinan univocament : dos ensembles coïncidisson se e solament se an lei meteisseis elements.
Çò qu'es important dins lo concèpte d'ensemble, es la relacion d’apartenéncia : un objècte apartèn a un ensemble (o au contrari li apartèn pas). En teoria axiomatica deis ensembles, qu'es a la basa de la presentacion axiomatica modèrna dei matematicas, se formaliza lei proprietats de la relacion d'apartenéncia.
Dins lo present article, se limitarem a un apròchi intuitiu dau concèpte d'ensemble : es lo ponch de vista de la teoria ninòia deis ensembles, sufisent dins la gròssa majoritat dei cas, maugrat l'existéncia de dificultats logicas que menèron a la constitucion dei teorias axiomaticas deis ensembles. En particular, la question de l'existéncia dei nocions introduchas (especialament : ensemble vuege, ensemble dei partidas, union, interseccion, diferéncia, e produch cartesian) que se pòt tractar solament dins lo quadre d'una teoria axiomatica, serà pas estudiada aicí.
Remarca terminologica : s'utiliza l'adjectiu ensemblista per qualificar çò que fa referéncia a la teoria deis ensembles (per exemple : definicion ensemblista).
Ensembles, elements e apartenéncia
[modificar | Modificar lo còdi]Segon lo ponch de vista «ninòi», se pòt considerar un ensemble coma un sac abstrach envoutant seis elements, çò qu'es ben representat per lei diagramas de Venn. Sovent (mai es pas totjorn possible), se destria tipograficament l'ensemble, notat per una letra latina majuscula coma « E » o « A », de seis elements, notats per de minusculas coma « x » o « n ».
Leis elements pòdon èsser de quina natura que siá : nombres, ponchs geometrics, drechas, foncions... Dins leis expausats elementaris, se balha volontiers d'exemples exteriors ai matematicas. Per exemple : diluns es un element de l’ensemble dei jorns de la setmana ; una bibliotèca es un ensemble de libres, etc.
Lo meteis objècte pòt èsser element de mai d'un ensemble : "4" es element de l'ensemble dei carrats perfèctes, e mai de l’ensemble dei nombres pars. Aquestei dos ensembles son infinits, valent a dire qu'an una infinitat d’elements.
L'apartenéncia d'un objècte, notat per exemple x, a un ensemble, notat per exemple A, s'escriu : .
Aquò se pòt legir ansin :
- « x apartèn a A »,
- « x es element de (l'ensemble) A »,
- « x es dins A »,
- « A a per element x ».
Per indicar la non-apartenéncia d'un objècte a un ensemble, se barra lo simbòl d'apartenéncia :
- « » significa : « y apartèn pas a A », « y es pas element de (l'ensemble) A » ...
Quauqueis ensembles importants
[modificar | Modificar lo còdi]L'ensemble vuege
[modificar | Modificar lo còdi]Una nocion comòda e importanta es aquela d'ensemble vuege, qu'a ges d'element (lo sac es vuege, segon la metafòra precedenta). Se designa per lo simbòl seguent : (o : ).
Principaus ensembles numerics
[modificar | Modificar lo còdi]Certans ensembles de nombres jògan un ròtle particularament important dins totei lei brancas dei matematicas :
- L'ensemble (o N) deis entiers naturaus
- L'ensemble (o Z) dei nombres entiers
- L'ensemble (o D) dei nombres decimaus
- L'ensemble (o Q) dei nombres racionaus
- L'ensemble (o R) dei nombres reaus
- L'ensemble (o C) dei nombres complèxes
Per exemple :
- , , mai .
- . Se saup que .
Egalitat de dos ensembles
[modificar | Modificar lo còdi]En matematicas, se considèra que dos objèctes son egaus quand lei proprietats de cadun d'elei son lei proprietats de l'autre, valent a dire que lei dos objèctes se pòdon pas destriar un de l'autre (es la definicion de Leibniz de l'egalitat).
En teoria deis ensembles, se considèra qu'un ensemble es completament determinat per seis elements, son extension. Per exemple, se pòt definir l'ensemble A deis entiers naturaus divisibles au còp per 3 e per 5 e l'ensemble B deis entiers divisibles per 15 : aquelei dos ensembles son egaus (tot element de A es element de B e tot element de B es element de A ), mai an de definicions diferentas.
Ansin, se dirà que dos ensembles A et B son egaus, e s'escriurà coma de costuma A = B, s'an exactament lei meteisseis elements, valent a dire se tot element de cadun d'elei es element de l'autre :
- se e solament se :
- onte « » designa lo qüantificator universau (legir : "per tot"), e « » designa l'equivaléncia logica.
En teoria deis ensembles, se conois aquesta definicion sota lo nom d'axiòma d'extensionalitat.
Definicion d’un ensemble
[modificar | Modificar lo còdi]Definicion en extension deis ensembles finits
[modificar | Modificar lo còdi]Se parla aicí d'ensembles finits en un sens intuitiu : un ensemble es finit s'existís un entier naturau ben determinat permetent de ne comptar totei leis elements (per exemple, l'ensemble dei jorns de la setmana es finit, que se pòt comptar seis elements sensa passar lo nombre 7).
Bòrd qu'un ensemble es completament determinat per seis elements, se pòt determinar un ensemble finit per una lista de seis elements, que se nòta entre acoladas. Se ditz que l'ensemble es definit en extension.
Per exemple :
- l'ensemble A que seis elements son 2, 3, e 5 es notat {2, 3, 5}
- l'ensemble dei jorns de la setmana es notat { diluns, dimars, dimècres, dijòus, divendres, dissabte, dimenge }
Remarquem que la notacion d'un ensemble definit en extension es pas unica ; en causa de la proprietat d'extensionalitat :
- l'òrdre d'escritura deis elements a ges d'importància :
- per exemple, se A = {2, 3, 5}, alora A = {2, 5, 3}, e tanben A = {5, 2, 3}, etc.
- l'escritura repetida d’elements entre leis acoladas modifica pas l’ensemble :
- amb lo meteis exemple, A = {2, 2, 3, 5}, A = {2, 5, 5, 5, 3}
Leis ensembles qu'an ren qu'un element son sonats singletons. Per exemple l'ensemble qu'a per solet element "2" es lo singleton notat {2}.
Definicion en comprension deis ensembles
[modificar | Modificar lo còdi]Un ensemble pòt èsser definit en comprension, valent a dire que se definís per una proprietat caracteristica de seis elements : es verificada per totei leis elements de l'ensemble e solament per seis elements. Per exemple, es clar que l'ensemble deis entiers naturaus premiers es definit en comprension, per la proprietat (relativa ais entiers naturaus) « aver exactament dos divisors ». Se pòt utilizar la notacion d'un ensemble definit en comprension [2], per exemple per l'ensemble deis entiers naturaus pars, s'escriurà :
- .
Se definirà parierament l'ensemble deis entiers comprés entre −7 et 23 :
- (lo simbòl logic "" se liège "e").
e l'ensemble dei carrats perfèctes non nuls :
Per aquest ensemble, se pòt adoptar una autra notacion, pus immediata :
- .
Existisson donc doas formas de notacion :
- per : « l’ensemble deis elements x de E que satisfàn la condicion P(x) »
- per : « l'ensemble deis imatges per l'aplicacion f deis elements x de E que satisfàn la condicion P(x) ».
Vaicí d'autreis exemples :
- es l’ensemble de totei leis entiers pars.
- es tanben l’ensemble de totei leis entiers pars.
- es l’ensemble vuege.
- es tanben l’ensemble vuege.
- es mai l’ensemble vuege.
- es l’ensemble dei nombres reaus.
- es l’ensemble dei matritz simetricas realas.
Relacions entre ensembles
[modificar | Modificar lo còdi]Inclusion, sosensemble
[modificar | Modificar lo còdi]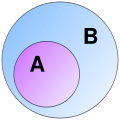
Estent dos ensembles A, B, se ditz indiferentament que :
- A es un sosensemble de B o A es una partida de B
- A es inclús dins B o A es contengut dins B o B contèn A
se totei leis elements de A son d'elements de B ; dins aqueu cas, s'escriu :
- .
Quauqueis exemples d'inclusions entre ensembles :
- , , e .
Proprietats
[modificar | Modificar lo còdi]- Per tot ensemble B, B es un sosensemble de B e l'ensemble vuege es un sosensemble de B :
- e .
- Transitivitat de l'inclusion : estent tres ensembles A, B, C,
- se e , alora .
Egalitat
[modificar | Modificar lo còdi]L'egalitat de dos ensembles es estada definida supra. Se pòt caracterizar ansin l'egalitat de dos ensembles A e B :
- se e solament se e
(valent a dire que tot element de A es element de B, e reciprocament tot element de B es element de A).
L'ensemble dei partidas
[modificar | Modificar lo còdi]Per tot ensemble A se definís l'ensemble dei partidas de A : es l'ensemble que seis elements son lei sosensembles de A ; se nòta . Per exemple, se A = { a, b, c } alora l'ensemble dei partidas de A es :
- .
Operacions binàrias entre ensembles
[modificar | Modificar lo còdi]Lei principaleis operacions binàrias ensemblistas son l'union, l'interseccion, la diferéncia (simetrica o non) e lo produch cartesian.
Union
[modificar | Modificar lo còdi]
L'union de dos ensembles A e B es l'ensemble constituit per totei leis elements qu'apartènon a l'ensemble A o a l'ensemble B o ai dos. Se nòta : A ∪ B.
- (lo simbòl logic "" se liège "o").
- Per exemple,
Proprietats
[modificar | Modificar lo còdi](Lei letras majusculas A, B, C designan d'ensembles).
- Relativas a l'inclusion:
- e
- se e solament se
- Commutativitat :
- Associativitat : ; per aquò, se nòta l'union sensa parentèsis :
Interseccion
[modificar | Modificar lo còdi]
L'interseccion de dos ensembles A e B es l'ensemble constituit per totei leis elements qu'apartènon simultaneament a l'ensemble A e a l'ensemble B. Se nòta : A ∩ B.
- (lo simbòl logic "" se liège "e").
- Per exemple,
Proprietats
[modificar | Modificar lo còdi](Lei letras majusculas A, B, C designan d'ensembles).
- Relativas a l'inclusion:
- e
- se e solament se
- Commutativitat :
- Associativitat : ; per aquò, se nòta l'interseccion sensa parentèsis :
- Distributivitats mutualas de l'union e de l'interseccion :
Diferéncia
[modificar | Modificar lo còdi]Diferéncia ensemblista
[modificar | Modificar lo còdi]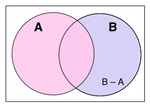
La diferéncia de dos ensembles A e B es l'ensemble constituit per totei leis elements de B qu'apartènon pas a A. Se nòta : B \ A o B − A.
- .
Quand A es una partida de E, la diferéncia ensemblista E \ A es tanben sonada ensemble complementari de A a respècte de E.
Per exemple, es l'ensemble dei nombres irracionaus (lei reaus que son pas racionaus).
Diferéncia simetrica
[modificar | Modificar lo còdi]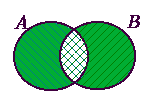
Se definís tanben la diferéncia simetrica de dos ensembles A e B, qu'es l'ensemble deis elements qu'apartènon a A e pas a B o ben qu'apartènon a B e pas a A (es a dire qu'apartènon a A o a B mai pas ai dos). Se nòta : A B.
- , e tanben .
Produch cartesian
[modificar | Modificar lo còdi]Lo produch cartesian de dos ensembles A e B es l'ensemble de totei lei pareus (a, b) taus que a ∈ A e b ∈ B. Se nòta : A B.
- .
Ensembles desjonchs
[modificar | Modificar lo còdi]Se ditz que dos ensembles A, B son desjonchs s'an pas d'element comun, valent a dire que :
Per exemple, l'ensemble dei nombres premiers diferents de 2 e l'ensemble deis entiers naturaus pars son desjonchs.
Se E, F son dos ensembles, e se A = E e B = F \ E, alora lei dos ensembles A, B son desjonchs.
Nòtas e referéncias
[modificar | Modificar lo còdi]- ↑ «Ensemble» (en francés). Multidiccionari Occitan Dicodòc. Congrès permanent de la lenga occitana. [Consulta: 8 de decembre de 2023]
- ↑ Apareis sota una forma un pauc diferenta dins leis Operazioni della logica Deduttiva (1888) de Peano.











































































