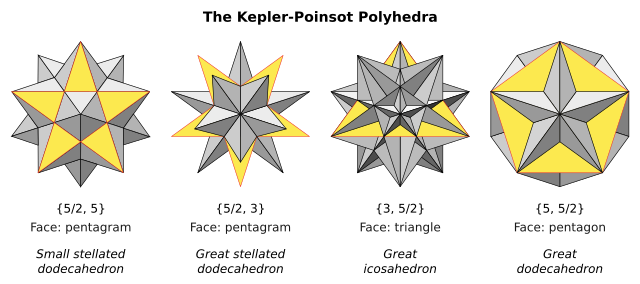
Solids de Kepler-Poinsot
Los quatre solids de Kepler-Poinsot son de polièdres que, en mai dels cinc solids platonics, se pòdon bastir de biais regular, dos d'aqueles que las fàcias son de poligòns regulars estelats (o crosats): los solids de Kepler, e dos avent de fàcias regulars, mas que pòdan s'interpenetrar: los solids de Poinsot.
- Lo pichon dodecaèdre estelat foguèt descobèrt per Kepler vint dos sègles aprèp Platon, en 1619. A dotze fàcias que son de pentagòns estelats, dotze vertèxes e 30 arèstas. Sus cada vertèxes se jonhan cind fàcias. Aquel pichon dodecaèdre estelat se pòt veire dins un mosaïc de Paolo Uccello, dins la basilica de Sant Marc de Venècia, realizada aproximativament en 1430 (o prèp de 200 ans abans sa descripcion matematica).
- Kepler tanben decobriguèt lo grand dodecaèdre estelat, format dels meteisses dotze pentagòns estelats, que a tanben 30 arèstas mas sonque 20 vertèxes.
- Poinsot descobriguèt lo grand dodecaèdre en 1809. Las seunas dotze fàcias son de pentagòns regulars, a 12 vertèxes e 30 arèstas. Mai de 200 ans avant, dins la seuna Perspectiva corporum regularium (Perspectivas dels solids regulars)[1], un libre de gravaduras sus fusta publicat en 1568, Wenzel Jamnitzer pintèt lo grand dodecaèdre.
- Descodriguèt fin finala lo grand icosaèdre, format de vint triangles equilaterals, e que possèda dotze vertèxes e 30 arèstas.
-
pichon dodecaèdre estelat {5/2, 5}
-
grand dodecaèdre estelat {5/2, 3}
-
grand dodecaèdre
{3, 5/2} -
grand icosaèdre
{5, 5/2}
Geometria
[modificar | Modificar lo còdi]| Nom | Imatge | Simbòl de Schläfli {p,q} |
Fàcias {p} |
Arèstas | Vertèx {q} |
χ | Simetria | Dual |
|---|---|---|---|---|---|---|---|---|
| Pichon dodecaèdre estelat | 
|
{5/2,5} | 12 {5/2} |
30 | 12 {5} |
-6 | Ih | Grand dodecaèdre |
| Grand dodecaèdre estelat | 
|
{5/2,3} | 12 {5/2} |
30 | 20 {3} |
2 | Ih | Grand icosaèdre |
| Grand dodecaèdre | 
|
{5,5/2} | 12 {5} 30px|Pentagòn |
30 | 12 {5/2} |
-6 | Ih | Pichon dodecaèdre estelat |
| Grand icosaèdre | 
|
{3,5/2} | 20 {3} |
30 | 12 {5/2} |
2 | Ih | Grand dodecaèdre estelat |
Lo pichon e lo grand dodecaèdre estelats an de fàcias en forma de pentacles no convèxes regulars. Lo grand dodecaèdre e lo grand icosaèdre an de fàcias en forma de pentagòns convèxes, mas an figuras de vertèx en forma de pentacles. Lo primièr parelh e lo segon son lo duals un dels autres.
La caracteristica d'Euler
[modificar | Modificar lo còdi]Un solid de Kepler-Poinsot cobrís la seuna esfèra circonscricha mai d'un còp. A causa d'aquò, son pas necessàriament topologicament equivalents a l'esfèra coma o son los solids platonics, e sobretot, la caracteristica d'Euler
- V - A + C = 2
es pas totjorn valida.
La valor de la caracteristica d'Euler χ depend de la forma del polièdre. Considerant per exemple lo pichon dodecaèdre estelat [1]. Es bastir per un dodecaèdre amb una piramida pentagonala sus caduna de las seunas dotze fàcias. Caduna de las dotze fàcias es un pentacle amb la part pentagonala amagada dins lo solid. La partida exteriora de cada fàcia es bastida de cinc triangles que se tòcan sonque en cinc punts. Alternativament, se poirián comptar aqueles triangles coma fàcias separadas - n'i a 60 (mas son pas que de triangles isoscèls, e non poligòns regulars). De biais similar, cada arèsta quedariá ara dividida en tres arèstas (mas alara, son de doas menas). Los "cinc punts" que s'acaban de mencionar, forman ensems los 20 vertèxes suplementaris, atal, i a un total de 32 vertèxes. Los pentegòns intèrnes amagats son pas necessaris per formar la superfícia del polièdre e pòdon despareisser. Ara, la relacion d'Euler es vàlida: 60 - 90 + 32 = 2. Mas, aquel polièdre es pas aquel descrich pel simbol de Schläfli {5/2,5}, e, pòt pas èsser un sòlid de Kepler-Poinsot encara qu'i ressembla de l'exterior.