Rectangle

En geometria, un rectangle es un quadrilatèr que los quatre angles son d'angles dreches.
Definidion e proprietats[modificar | Modificar lo còdi]
Un quadrilatèr es una figura plana constituida per quatre vertèxes e de quatre segments (o costats) ligant aqueles verxess dos a dos de biais a terminar un entorn tancat.
-
Quadrilatères. Los dos situats en naut a esquèrra son de rectangles.
-
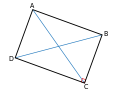
Un rectangle, las seunas doas diagonalas e un angle drech.
Mostrar qu'un quadrilatèr es un rectangle[modificar | Modificar lo còdi]

Diferentas proprietats caracteristicas permetan d'afirmar qu'un quadrilatèr es un rectangle.
Sufís qu'un quadrilatèr possedís tres angles dreches per èsser un rectangle.
S'un quadrilatèr es un parallelograma, alara qu'es un rectangle se una de las proprietats segentas se verifica:
- possedís dos costats consecutius perpendiculars (es a dire que possedís un angle drech);
- la seunas diagonalas an la meteissa longor.
Proprietats[modificar | Modificar lo còdi]
Los costats oposats d'un rectangle son parallèls e de meteissa longor; sas diagonalas son de meteissa longor e se copan al mitan.
Lo rectangle possedís dos axes de simetria, que son las mediatriças de sos costats. possedís tanben un centre de simetria, l'interseccion de las seunas diagonalas.
Las diagonalas essent de meteissa longor e secantas al mitan O, los quatre vertèxes del rectangle son equidistents d'O, çò que significa qu'existís un cercle de centre O passant per aqueles quatre vertèxes, nomenat cercle circonscrich al rectangle, qu'es desperel dich inscrich dins aquel cercle.
Quin que siá rectangle, pòt servir a constituir un pasiment del plan. Aquò vòl dire qu'es possible, amb de rectangles identics, de cobrir tot lo plan sens superpausar dos rectangles. De drechas perpendicularas partatjant lo plan en zonas rectangularas.
Mesuras[modificar | Modificar lo còdi]

| Perimètre | 2 × (a + b) |
| Aira | a × b |
| Diagonala |
Los costats d'un rectangle essent dos a dos de meteissa longor a e b, es d'usatge de nomenar dimensions del rectangle aqueles dos nombres. Lo mai grand es la longor del rectangle, le mai pichon la largor.
Un rectangle de costats a e b possedís un aira egala a a × b, e un perimètre de 2 × (a + b).
L'applicacion del teorèma de Pitagòras permet de constatar que las diagonalas del rectangle son egalas e mesuran
Dos rectangles qu'an meteissa longor a e meteissa largor b son isometrics. Aquò significa que son superposables: l'un dels dos pòt èsser transformat en l'autre per une succession de translacions, rotacions o capviraments. Lo quocient a⁄b es nomenat format del rectangle. Totes los rectangles de formats egals son semblables: existís un agrandiment (o una reduccion) permetent de passar de l'un a l'autre. O encara, an « la meteissa forma ». Coma la longor es superiora o egala a la largor, lo format es un nombre superior o egal a 1. Un format egal a 1 es caracteristic d'un carrat. Mai lo format es grand, mai lo rectangle es « alongat ».
Rectangles remarcables[modificar | Modificar lo còdi]
Carrat[modificar | Modificar lo còdi]
Un carrat es un rectangle particulièr que los quatre costats an la meteissa longor.
Rectangle d'aur[modificar | Modificar lo còdi]
Vejatz tanben[modificar | Modificar lo còdi]
- Bibliografia: (fr) Patricia Rulence-Pâques, Perception de surface et inférence de surface : le cas de la surface du rectangle, EHESS, Universitat París 5, 1996 (tèsa de doctorat de Psichologia)