Espaci vectoriau
Aparença
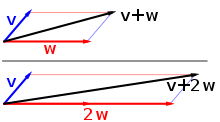
Un espaci vectoriau es un ensemble d'objèctes matematics, dichs vectors, que pòdon èsser addicionats entre elei e que pòdon èsser multiplicats per un escalar. Es ansin un ensemble dotat d'una estructura permetent de realizar de combinasons linearas. Leis escalars son generalament de nombres reaus ò complèxes. Per aquela rason, la definicion de l'estructura d'un espaci vectoriau sus un còrs K es una nocion de basa de l'algèbra car a d'aplicacions importantas dins d'autrei disciplinas scientificas.
