Èrsa

Èrsa salivant sus la còsta salvatja de l'illa d'Yeu.

Èrsas dins l'Atlantic Nòrd - nau dins la tempèsta.

Una èrsa, una ondada o una onda es una deformacion de la superfícia d'una massa d'aiga mai sovent causada pel vent. A l'interfàcia dels dos fluids màger de la Tèrra, l'agitacion de l'atmosfèra provòca sul oceans, mars e lacs, de movements de superfícia jos la forma de successions d'ondas, de mèsme anar mas diferentas. Los seïsmes màger, erupcions volcanicas o casudas de meteoritas crean tanben d'èrsas nomenadas tsunamis o onda de mar. La marèa es tanben a l'origina d'ondas plan particularas, nomenadas mascarets, que se produson dins las escasenças ont l'onda de marèa encontra un corrent opausat e de velocitat egala. Unes fenomèns meteorologics pòdon èsser a l'origin de tsunamis meteorologics, que l'èrsa pòt aver las mèsmas caracteristicas qu'aquesta d'un tsunami.

Los trins d'ondas provocats pel vent se propagan en se dispersant, las èrsas mai arcadas pòdon de rompre creant de turbuléncias e de corrents marins. S'agís d'ondas de gravetat, la fòrça de rampèl essent la pesantor: lor evolucion es determinada per las proprietats comunas a las ondas coma lo rebat, la refraccion e la difraccion.

La nautor de las èrsas varia d'unes centimètres fins 32,3 m per la mai nauta registrada per un instrument, veire mai de 34 m per la mai nauta observada visualament e 36 m de maxim extrapolats d'una mejana de 20,1 m pendent de la tempèsta Quirin en febrièr de 2011.

La descripcion mai elementària d'aqueste fenomèn complicat repausa sus la nocion de nautor significativa d'un estat de mar. Quand la nautor d'una èrsa individuala passa excepcionalament aquesta nautor se dich « èrsas gigantas » podent causar de domatges importants a las naus que'n son surpresas.

Representacions matematicas

L'astronòm et matematician George Biddell Airy donèt la teoria mai simpla per d'ondas regularas (periodicas). L'onda d'Airy ten una superfícia liura de forma sinusoïdala. S'agís d'una representacion plan simplificada de la realitat, valabla en principi per d'ondas regularas de fèbla arcadura. L'arcadura es definida coma lo rapòrt de la nautor sus la longor d'onda. Aquesta teoria es pasmens eficaça per resòlvre fòrça problèmas practics, a condition de saber associar de caracteristicas pertinentas al fenomèn natural fòrça mai complicat que serà descrich çai dejós.

Se miram amb atencion las èrsas en mar, constatam que gaireben totas son pas sinusoïdalas: las crèstas son mai punchudas, los clòts mai plans. Aqueste aspècte es intergrat en remplaçant l'aproximacion d'Airy, al primièr òrdre, per d'aproximacions periodicas d'òrdre superior sovent atribuidas a Stokes.

Estampa japonesa, extracha de las trenta e sièis vistas del Fuji de Katsushika Hokusai

Observant la succession de las ondas, s'apercep que presentant gaireben pas de regularitat; jamai i a doas èrsas identicas. Alara se descriu l'estat de la mar de biais estatistic. Un modèl simple repausa sus l'analisi espectral qu decompausa la superfìcia de la mar en una soma d'una infinitat d'ondas infinidament pichonas avent la mèsma direccion. Aquesta descripcion basada sus una simpla somma d'ondas d'Airy pren pas en compte las non linearitats introduchas per Georges Stokes, imperfeccion que se pòt satisfar mai sovent.

Per de prigondors fòrça mai pichonas que la longor d'onda e per unas aplicacions en granda prigondor, subretot per la mar del vent, la superposicion d'ondas d'Airy es pas mai pro precisa. Se pòt alara utilizar diferentas tecnicas coma la transformacion de Creamer, o los modèls espectrals d'òrdre superior. La sola dificultat que siá pas encara resolguda es la representacion fidèl del desplegament.

Sens aver recors a aquestes modèls mai complèxes, es sovent util de se'n tenir a una onda lineària e periodica de mèsma energia. En efièch, per d'ondas lineàrias, las proprietats quadraticas que son l'energia o la deriva de Stokes s'adicionan. Se pòt atal deduire l'essencial de las proprietats (nautor, velocitat de las particulas, pression…) associadas a las èrsas irregularas per la raíç de la soma dels carrats d'aquestas mèmas proprietats per d'èrsas regularas.

Propagacion de las ondas

Coma totas las menas d'ondas, subretot las ondas luminosas descrichas per l'optica, la èrsas pòdon se rebatre, se difractar e se refractar. aquestes fenomèns, aisits de caracterizar per d'èrsas regularas, se complican per las èrsas naturalas tot demorant qualitativament analogas. A la diferéncia dels fenomèns luminoses, las èrsas an de longors d'onda a nòstra escala, çò que facilita la compreneson.

Rebat

Mar brescada. Punta de las Balenas, illa de Re

Lo rebat se realiza sus un obratge de nautor immergida importanta al respècte de la prigondor e de largor importanta al respècte de la longor d'onda.

Quand d'èrsas arriban en parallel a una levada se produch un rebat total, fenomèn d'onda estacionària. Sus la paret e a de distàncias proporcionalas a la mièjalongor d'onda s'obsèrva de ventres ont l'amplitud es lo doble de l'amplitud incidenta. Entre dos ventres successius i a un nos ont l'agitacion sembla desapareisser.

Davant una levada de riba se produch un rebat parcial amb de ventres que l'amplitud es inferiora al doble de l'amplitud incidenta alara que los noses an pas mai una amplitud nulla.

Se las èrsas arriban de biais la superposicion d'ondas incidentas e rebatudas produch una mar brescadas.

Difraccion

Los fenomèns se complican al vesinat d'un obstacle de dimensions pro pichon al respècte de las longors d'onda, coma una nau, o del tèrme d'una levada

Fàcia a un obstacle, l'aproximacion de l'optica geometrica descriu lo comportament de la lutz a las escalas superioras a las longors d'onda, çò que fa apareisser una zona d'ombra rèire l'obstacle. Los obstacles encontrats per las èrsas avent sempre de dimensions de l'òrdre de las longors d'onda, cal utilizar la nocion de difraccion segon que produch sempre una agitacion dins l'ombra geometrica.

Refraccion

La diminucion de la celeritat amb la prigondor mena a de fenomèns de refraccion que s'interprètan simplament remarcant que la longor d'onda varia de biais proportcional a la celeritat. Un element de crèsta arribant de biais al respècte de las isobatas (linhas d'egala prigondor) possedís una extremitat que se trapa sus une prigondor inferiora a aquesta de l'autra extremitat. Las longors d'onda essent diferentas la crèsta bascula fins a s'aprochar de la direccion de l'isobata. De biais imatjat se dich que los nauts fonds frenan las èrsas.

Sus una plaja, las crèstas s'aprochan donc de la linha de riba fins a que la prigondor siá pro fèbla per que comença lo desplegament. Sus una punta i a concentracion de las ortogonalas (analògs als rais luminoses), donc aumentacion de l'agitacion e una atenuacion ligada a l'espelida dins una baia. Lo contornament d'una illòta pòt crear dins l'« ombra geometrica » un aument de l'agitacion per superposicion d'èrsas venent de dos costats.

Los corrents modifican tanben la velocitat de fasa e la relacion de dispersion. Induson donc tanben una refraccion.

Èrsas regularas e èrsas irregularas

La nocion d'èrsa regulara permet de resòlvre un cèrt nombre de problèmas pasmens que siá pro alunhada de la realitat fisica. En efièch, lo vent bufant sus la superfícia de la mar crea una agitacion erratica: es la mar del vent. Pendent la propagacion, la dispersion d'èrsas fòra de la region de generacion fa qu'aquestas prenon una aparéncia sempre mai regulara. Aquesta ondada s'aprocha de l'onda regulara sens i capitar que perd de compausanatas sens pas jamai venir un fenomèn monocromatic.

Èrsas regularas en prigondor constanta

Problèma

Domèni de validitat de las teorias aprochadas per las ondas regularas, en foncion de la prigondor h, nautor de l'onda H, periòde temporal de l'onda τ e pesantor g.

Una èrsa periodica es caracterizada per

• la prigondor $h$,
• la nautor de crèsta de clòt $H$ o l'amplitud $a$ qu'es la mitat d'aquesta,
• e la longor d'onda $\lambda$ o lo nombre d'onda $k=2\pi /\lambda$.

En nombres sens dimension es caracterizada per

• la cambradura $H/\lambda$ o lo produch $ka$
• e la prigondor relativa $h/\lambda$ o lo produch $kh$.

Aquesta descripcion correspond a una modelizacion grossièra qu'ignora las irregularitats de las èrsas de la natura e lor aspècte tridimensional. Supausa tanben una prigondofor constanta pasmens se'n balhe en fòrça escasenças una aproximacion rasonabla.

Relèva del problèma mai simple de la mecanica dels fluids qu'ignora la viscositat, la compressibilitat, l'existéncia de remolins (escorriment irrotacional d'un fluid incompressible e perfièch). Dins aquestas condicions la descripcion euleriana classica del camp de las velocitats se reduisís a la recerca d'un potencial armonic. Lo caractèr non linear de la condicion a la superfícia liura interdich pasmens la recerca de solucions simplas encontradas dins d'autres problèmas fisics.

Unes tipes d'aproximacions son utilizats.

• Las equacions de Boussinesq son utilisablas per d'ondas de fèble amplitud.
• Las aproximctions de Stokes convenon per de prigondors relativament importantas al respècte de la longor d'onda.
• Las equacions de Barré de Saint-Venant son adaptadas e de fèblas prigondors ont se pòt far l'ipotèsi de l'equilibri idrostatic.
• Las aproximacions utilizant la foncion de corrent son formalament identicas a las aproximacions de Stokes mas obtengudas per un metòde de mendres carrats puslèu qu'un desvelopament limitat. Lo calcul numeric permet de satisfar gaireben exactament la condicion dinamica (l'error tolerada pòt èsser tan pichona que se vòl) e exactament totas las autras condicions, quina que siá la prigondor.

Lo diagrama descriu dins un plan (prigondor relativa/cambradura) lo domèni de validitat de diferentas aproximacions de tipe desvelopament limitat bornat per la cambradura limita al delà de que l'èrsa rompa. Mai precisament la prigondor e la nautor son raportadas e la longor d'onda en prigondor infinida multiplicada per $2\pi$.

Aproximacions de Stokes

Una solucion naturala consistís a exprimir lo potencial e, enseguida, las diferentas grandors per de desvelopaments limitats en foncion del paramètre $ka\,$, es a dire de la cambradura supausada pichona.

Prenant que lo primièr tèrme del desvelopament s'obten un modèl linear pels camps de velocitat e pression, conegut jol nom d'onda d'Airy, qu'es donc valable en principi sonque per las èrsas de cambradura infinidament pichona, totes los tèrmes suprimits essent alara d'infinidament pichons d'òrdres superiors, donc de negligir. Presenta doas caracteristicas:

• La superfícia liura es sinusoïdala.
• Las trajectòrias de las particulas fluidas son ellipticas.

Per de rasons de simplicitat, l'onda d'Airy es sovent utilizada al delà de son domèni de validitat teorica. Son caractèr lineari permet de superpausar las solucions, e de constituir atal un estat de mar pro realista jos la forma d'une soma d'èrsas de diferents periòdes e direccions.

Del moment que la cambradura es pas plan pichona pòt èsser preferible, per fòrça calculs mai laborioses, d'utilisar de modèls d'ondas d'amplitud finida obtenguts apondant de correccions d'òrdres superiors. Melhoran lo realisme que concernís los dos punts precedents.

• A mesure que los òrdres d'aproximacion s'auçan a la superfícia liura presenta de crèstas sempre mai ponchudas e de clòts sempre mai plans. L'aproximacion del cinquen òrdre es mai sovent jutjada pro realista per la descripcion de las èrsas regularas, levat quand l'èrsa s'apròcha de la cambradura maximala.

• Un tèrme de deriva proporcional al carrat de l'amplitud deforma las trajectòrias ellipticas del primièr òrdre per far naícer de trajectòrias que semblan mai o mens a de cicloïdas alongadas. Un metòde elegant permet de determinar aquesta deriva corrigissent lo camp de velocitat d'Euler per un calcul dins las coordonadas de Lagrange. Pasmens la coeréncia del desvelopament limitat exigís qu'aquesta correccion siá considerada coma un tèrme del segond òrdre de negligir al primièr òrdre.

Approximacions en aiga pauc prigonda

mouvement et dérive des particules en faible profondeur

Lo desvelopament limitat de Stokes pèrd de sa significacion quand la prigondor relativa ven inferiora a 1/8 environ. Dins aquestas condicions s'obsèrva de crèstas plan ponchudas separadas per de clòts plan espandits. Aqueste fenomèn es pres en compte pel modèl de l'onda cnoïdala que tend cap a doas limitas:

• L'onda d'Airy quand la nautor es pichona al respècte a la prigondor.
• L'onda solitària quans la longor d'onda es granda al respècte de la prigondor. L'onda que se situa alara entièrament al dessus del nivèl de repaus presenta pas mai de periodicitat.

Aproximacions de la foncion de corrent

Lo modèl cnoïdal es gaire pas adaptat a las èrsas de fòrtes cambraduras.

Lo metòde utilizat es un pauc analòg a aqueste de las aproximacions de Stokes amb doas diferéncias. La foncion de corrent remplaça lo potencial e s'agís mai d'un desvelopament limitat clasic que que negligís los tèrmes d'òrdres superiors. Un còp causit lo gra de l'aproximacion, los coeficients son determinats en minimizant l'error al sens del metòde dels mendres carrats.

Aqueste metòde desvelopat per Dean puèi Dalrymple (1974) pòt donar d'aproximacions melhoras qu'aquestas que precedisson. Se pòt atal trapar la forma de l'èrsa de cambradura maximala, que presenta una crèsta punchuda formant un angle de 120°.

Instabilitat de las èrsas periodicas

En practica las èrsas son pas jamai exactament periodicas, e tanben en laboratòri, que las solucions matematicas periodicas son instablas: las ondas evoluan cap a d'autras formas, amb de trins d'èrsas irregularas (instabilitat modulacionala de Benjamin e Feir) o cap a la salivada (instabilitat de la crèsta, mostrada per Tanaka). Fòrça autras instabilitats existisson que pòdon crear espontanèament de formas en tres dimensions (èrsa en fèrre de caval per exemple).

Propagacion de las èrsas (modèl d'Airy)

La primièra aproximation de Stokes, a l'òrdre 1 en foncion de ka, dona la teoria lineara de las èrsas, tanben nomenat modèle d'Airy. Es particularament pan adaptat per descriure las ondadas de fèble cambradura, per de prigondors grandas al respècte de l'amplitud de las èrsas.

Onda d'Airy d'un periòde de 2 segondas per 3 mètres de fons. A esquèrra: velocitat e variacions de pression, a drecha: trajectòria de particulas pendent 4 segondas.

Relacion de dispercion

Lo movement de las ondas se pòt considerar coma irrotacional, deriva donc d'un potencial. Coma l'aiga es gaireben incompressibla, aqueste potencial satisfach l'equacion de Laplace. Per las longors d'onda superioras a 30 cm, la tension superficiala se pòt negligir, e las solucions periodicas de fèble amplitud (ondas d'Airy) obesisson a una relacion de dispersion:

${\omega }^{2}=g\,k\,\tanh(k\,h)$,

amb

• $\omega =2\pi /T$ la pulsacion de l'onda,
• $T$ lo periòde de l'ondada,
• $g$ l'intensitat de la pesantor,
• $k=2\pi /L$ lo nombre d'onda,
• $L$ la longor d'onda de l'ondada,
• $h$ la prigondor de l'aiga.

Aquesta relacion dona la celeritat de propagacion de l'onda:

$c={\frac {\omega }{k}}={\sqrt {{\frac {g}{k}}\tanh(k\,h)}}$

Per d'onda regularas, aquesta relacion es corrècta à 10 % près en aiga prigonda, e l'error pòt aténher 30 % en aiga pauc prigonda. En efièch la celeritat tanben aumenta amb l'amplitud de las ondas.

Constatam que la velocitat de las ondas aumenta amb lo periòde: las ondas se dispersan, levat dins la limita de las fèblas prigondors. Atal los trins d'ondas mai longs provocats per una tempèsta arriban abans las ondas mai cortes. Per las grandas prigondors (al delà de la mitat de la longor d'onda), la velocitat de las ondas depend mai de la prigondor que la tangenta iperbolica tend cap a 1.

La relacion de dispersion permet tanben de comprene lo comportament de las èrsas prèp del litoral. Quand la prigondor diminís espacialament, lo periòde demora constant. Las formulas çai dessús provòca l'aument del nombre d'onda, donc la diminucion de la longor d'onda e de la celeritat.

Per simplificar, dins lo cas de l'aiga prigonda:

• celeritat (velocitat de propagacion o velocitat de fasa) en m/s: $c=1,25{\sqrt {L}}$;
• periòde (temps que separa doas crèstas): $T\approx 0,8{\sqrt {L}}$;
• longor d'onda: $L\approx 1,6T^{2}$.

Velocitat de grop

La velocitat de grop $C_{g}\,$, velocitat del transpòrt d'energia varia de biais mai complèxe. Partant de l'aiga prigonda $C_{g}\,$ aumenta de 20 % gaireben abans de decreisser ela tanben. Per grands fons $C_{g}=C/2$. Atal las ondas van mai aviadament que los grops: naisson al rèire del grop, lo passan e morisson a l'avant del grop. Per pichons fons $C_{g}=C$, e las ondas son pas mai dispersivas.

Energia e velocitat de deriva

La quantitat d'energia mecanica per unitat de superfícia de la mar (se dich densitat espaciala de l'energia) es, en mejana sul periòde de las ondas, egala a $E_{t}=\rho ga^{2}/2\,$, dins lo cas de las ondas d'Airy. Aquesta densitat s'exprimís en jolas per mètre carrat, e es la soma de l'energia potenciala e energia cinetica. Quand las ondas se propagan frontalament cap la còsta, lo flus d'energia per unitat de longor de crèsta es $C_{g}E_{t}$. Sens dissipacion d'energia e sens corrents, aqueste flus es constant. D'ondas que se propagan cap a la còsta veson donc lor nautor $2a\,$ diminuir gaireben de 10 % abans d'aumentar fins a qu'acaban per se rompre, qunas la velocitat de las particulas d'aiga atenhon la velocitat de fasa de l'onda que los pòrta.

Las ondas son tanben associadas a una deriva. Sus l'ensemble de la colomna d'aiga aquesta deriva dona un debit de massa egala a $E_{t}/C\,$, que s'exprimís en quilogramas per mètre. Aqueste debit es la quantitat de movement del camp d'onda. La realizacion d'aqueste debit, pendent la propagacion, demanda un flus de quantitat de movement: atal las ondas pòrtan la quantitat de movement dempuèi la region ont lo vent los engendrèt, fins a las còstas ont aquesta quantitat de movement es transmesa al corrent litoral.

Una èrsa formada per un fèrri

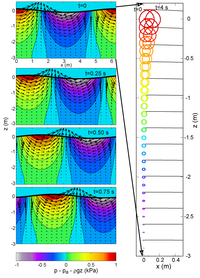
Movement del fluid

Dins la teoria d'Airy, las particulas de fluid descrivon d'ellipsas gaireben tancadas, que la talha decreis amb la prigondor. En aiga prigonda (prigondor superiora a la mitat de la longor d'onda) aquestas ellipsas son de cercles.

Lo fach que las ellipsas sián gaireben pas tancadas es une manifestacion de la deriva de Stokes. Près de la superfícia liura, la velocitat d'una particula d'aiga es mai importanta jos una crèsta que la velocitat opausada pendnet lo passatge del clòt venent. Ne resulta una deriva dins lo sens de propagacion d'ondas que pòt capvirar en prigondor. Per las ondas engendradas pel vent, aquesta deriva es de gaireben 1,5 % de la velocitat del vent per un estat de mar complètament desvelopat e en aiga prigonda.

Validitat e limitacions

Per una onda presa individualament, l'aproximacion d'Airy es particularament plan verificada dins lo cas d'una ondada constituida per d'ondas pauc cambradas se propagant al larg e somesas a pauc de vent. A mesura que la cambradura aumenta, ven sempre mai imprecisa mas es pasmens sovent utilizada a causa de sa simplicitat. Per de problèmas qui demandan una granda precision, l'amplitud de las ondas podent demandar una aproximacion superiora utilizada.

L'aproximacion d'Airy, ven fòrça imparfiècha dins las fèblas prigondors e se la due remplaçar per exemple per l'aproximacion cnoïdala. Es tanben imparfiècha dins una zona de ropmpadura, que siá dins la zona de generacion de la mar del vent o suls nauts fons.

Fin finala, per d'estats de mar reals (irregulars), se pòt obtener las caracteristicas d'ondas en superpausant un grand nombre d'ondadas d'Airy. Aquí tanben, se pót utilizar des correccions non lineara per tornar trobar de clòts mai plans que las crèstas (correccion de Creamer per exemple).

Salivada

Dins l'ensemble de las ondas engendradas pel vent, o dins los trins d'ondada se propagant per pichons fons o contra de corrents advèrses, unas ondas son tròp cambradas per èsser establas: se rompan.

Près d'un rivatge, a mesura que la prigondor diminuís, la forma de las ondas se modifica, primièr gaireben de biais simetric puèi en general amb una fàcia avant sempre mai règda fins l'instabilitat que se produch quand la nautor de l'onda es del mèsme òrdre que la prigondor. Quand l'onda saliva, l'essencial de son energia es dissipada en remolin e formacion de bofigas d'aire. La quantitat de movement qu'èra associada a l'onda contribuís a accelerar lo corrent dins la direccion de la salivada.

La forma d'una salivada al vesinat de la riba depend subretot del penjal de fons. Anant dins lo sens dels penjals creissents se destria mai sovent tres tipes de salivadas. La salivada progressiva o limpanta (spilling breaker en anglés) se produch mai sovent ss las plajas de fòrça fèble penjal. Las ondas començan salivar luènh de la riba amb una crèsta d'aspècte escumós qu'aumenta pendnet de la progression daissant en rèire una sisa d'escuma.

La salivada cabussanta (plunging breaker en anglés) es fòrça espectaculara amb de rotlèu qu'agradan los surfaires. L'èrsa s'enròtla a l'entorn d'una pòcha d'aire puèi s'aclapa creant un regiscle notable. Aquò ten a se produire mai sovent sus un penjal fòrt o sus un cambiament subte de la prigondor (un relaisset rocasut o un estèu). I a fòrça mai d'energia dissipada que d'energia rebat sus la plaja.

La salivada frontala o conflanta (surging breaker en anglés) se forma coma la salivada cabussanta mas l'èrsa puja la plaja avant que la crèsta se pòsca enrotlar. La zona de cabussada es fòrça estrecha e una granda partida de l'energia es rebatuda capa a las mai grandas prigondors.

Unes considèran tanben un cas intermediari entre las salivadas cabussant e conflanta (collapsing breaker). Puslèu de constituir un ròtleu, l'èrsa presenta una fàcia verticala abans de s'aclapar.

Èrsas irregularas

Descripcion estatistica

Observacions visualas

Las primièras donadas chifradas sus l'agitacion en mar foguèron lo resultat d'observacions visualas. L'observaire anonciava après unas minutas una nautor d'ondas, nomenada nautor significativa, e, mai rarament, un periòde mejan.

Aquesta observacions foguèron primièr realizadas per bastir d'estatisticas relativas a de sites donats. Son enseguida sistematizadas sus de naus, los resultats essent alara gropats per zonas geograficas.

Enregistraments analogics

La realizacion de captor d'ondadas associats a d'enregistraires sus papièr mostrèt l'evolucion de la superfícia liura pendent un enregistrament. Aquò permetèt de realizar un istograma de nautors d'ondas. Es alara mostrat que la mejana del tèrç de las nautors mai fòrtas essent pròche de la nautor significativa anonciada per un observator entraïnat, çò que constituís una definicion mai racionala.

Enregistraments numerics

L'informatica foguèt a l'origina de progrès espectaculars mercé a l'utilizacion d'enregistraments de mòstras.

Lo calcul de l'desviacion tipica de las mòstras, nomenat mejana quadratica en matèria de senhals, mòstra qu'es prèp del quart de la nautor significativa ja definida, çò que mena a una novèla definicion levada d'ambiguïtat.

L'istograma de las mòstras sembla mai o mens a un istograma normal o istograma de Gauss. Es confòrme al teorèma central limita que s'agís de la soma d'un grand nombre de tèrmes mai o mens independents. Es particularament plan verificat amb una ondada pauc cambrada. Dins la mar del vent las ondas cambradas presentan una dissimetria de las crèstas e de clòts analògs a aquesta qu efoguèron evocada al respècte de las ondas regularas. Coma dins fòrça domènis aquesta distorsion es negligida a causa de l'eficacitat de la lei de Gauss.

Descripcion espectrala

Metòdes

L'analisi espectral amassa diferents metòdes de representacion d'un senhal per una soma de sinusoïdas.

Lo desvolopament en seria de Fourier representa un senhal periodic per una soma de sinusoïdas d'amplituds finits que las frequéncias son los multiples de l'invèrs del periòde. Las descripcions de Stokes de las ondas regularas son constituidas pels primièrs tèrmes de tals desvelopaments.

La transformacion de Fourier permet de descriure un senhal transitòri. L'idèa consistís a realizar un desvelopament en seria de Fourier d'un troç quin que siá del senhal que se fa tendre la longor cap a l'infinit. Las frequéncias de las compausantas s'apròchan de biais indefinit alara que lors amplituds tendon cap a zèro. Multiplicant per la longor d'analisi s'obten per cada frequéncia un resultat finit nomenat densitat d'amplitud. Pasmens que sián de nocions fisicas sens rapòrts, lo parelh amplitud/densitat d'amplitud es formalament de mèsma natura que lo parelh carga concentrada/carga repartida de la flexion (material).

Aquesta darrirèa tecnica es en principi aplicabla a l'enregistrament d'una tempèsta en mar que possedís un començament e una fin fòrça plan identificats. Malaürosament l'informacion obtenguda a la seguida de calculs importants es dificil a interpretar. Es preferable d'utilizar un metòde un pauc mai abstrach, tanben encontrat per las vibracions, que provesís a mendre cost d'informacions mai utilizablas.

Cas de las èrsas

L'idèa consistís a remplaçar lo fòrça long enregistrament per una sequéncia d'enregistraments disjonchs, per exemple d'un vintenat de minutas cada les tres oras.

La succession d'enregistraments dona una idèa rasonabla sus l'evolucion de la tempèsta (o de tot autre estat de mar) alara que cadun d'eles es supausat pro long per provesir una informacion estatisticament significativa mas pro cort per que lo nivèl d'agitacion aja pas tròp evoluat. L'enregistrament es atal considerat coma una partida d'un senhal qu'evolua pas pendnet un temps infinit. Aquestas consideracions pro foscs son precisadas per la nocion de procés estacionari.

Que que siá, la sola informacion segura sul fenomèn demora dins l'enregistrament. Se pòt traduire dins lo domèni de las frequéncias utilizant la transformada de Fourier de l'enregistrament completada per de zèros als epòcas ont lo fenomèn foguèt pas registrat. S'i a de rasons de creire que lo senhal èra efectivament nul fòra de l'enregistrament la transformacion de Fourier lo traduch perfièchament. S'es de tipe transitòri amb de l'informacion perduda la densitat d'amplitud ne dona la melhora aproximacion. Dins le cas de las èrsas aquesta aproximacion a pas mai de sens mas un analisi mai prigonda mòstra que la representacion corrècta utiliza la densitat espectrala que se deduch de la densitat d'amplitud.

L'error ligada a la pèrda de l'informacion situada fòra de l'enregistrament se traduch per un filtre que torna organizar sogon la frequéncia tot coma la densitat espectrala que la densitat d'amplitud. Dins lo cas de la èrsas s'apond una incertitud ligada al fach que dos enregistraments de mèsme longor realizats a d'epòcas diferentas donan pas exactament lo mèsme resultat.

Utilitat de la densitat espectrala

Quand una èrsa excitís un sistèma mecanic linear (per exemple una nau) la densitat espectrala de sa responsa (per exemple lo brandament de la nau) se deduch de la densitat espectrala de l'excitacion per l'intermediairi de la foncion de transferiment del sistèma.

Se l'excitacion es considerada coma una realizacion d'un procediment de Gauss la responsa del sistèma lineari possedís la mèsme proprietat. Dins aquetas condicions la densitat espectrala permet d'estimar la distribucion dels amplituds de crèstas, lo periòde mejan de passatge al zèro, lo periòde mejan de cresta, etc.

Generalizacion

La densitat espectrala sufís per descriure una ondada epurada per son trajècte que possedís de crèstas quasirectilinhas. Dins la zona de eneracion s'observa d'ondas de cortas crestas. Aquestas pòdon se descriure coma de somas d'èrsas sinusoïdalas que son diferentas per lor frequéncias mas tanben per lors direccions, çò que mena a la nocion de densitat espectroangular.

Fòrça d'èrsas e ressac

L'ingenhaire escocés Thomas Stevenson realiza en 1843 un dinamomètre enregistraire epecial per mesurar la fòrça de las èrsas sus una superfícia verticala. Mòstra atal que la pression de l’aiga suls bauces, que varia amb lo tipe d'èrsas e la prigondor, pòt aténher 30 tonas / m² pendent las ventadas d'ivernalas.

Lo ressac es lo retorn violent d'èrsas sus ela mèsmas que saliva contra un obstacle. Exercís un efièch de chucament, agissant sul transpòrt, los enlevaments e los depauses marins.

Per l’estimacion de la fòrça d'una èrsa, se destria las èrsas salivantas e las ondadas. La determinacion de las fòrça exercidas per las èrsas sus d'estructuras son de problèmas complèxes que son o resolgut experimentalament o sempre mai a de simulacions numericas coma amb lo logicial OpenFOAM per exemple.

Èrsa salivanta

Una èrsa salivanta es un fenomèn idrodinamic non linear, non estacionari que depend del penjal del fons e de la natura de l'ondada al larg. Tres modèls teorics principals permetent d'estimar la fòrça d'una èrsa salivanta: lo tust per còp de moton, lo tust ventilat e lo tust per compression.

Unas equacions permeton d'estimar la fòrça de l'accion de las èrsas dins de cas particulars. Per exemple, lo metòde de Minikin per la fòrça maximala d'una èrsa sus una paret verticala.

Ondadas

Las fòrças exercidas per las ondadas sus d'estructuras immergidas es un problèma complèxe d'idrodinamic. Los calculs demandan d'estudis estatisticas de las ondadas, devon prene en compte los diferents aspèctes de la fòrça que la traïnada, los efièch cumulatius de las èrsas, los efièchs de la difraccion de l'ondada per las estructuras fixas etc.

L'èrsa dins los domènis artistics

Las èrsas inspirèron fòrça artistas.

• 
  L'èrsa de Guillaume Seignac, vèrs 1908.
• 
  L'Èrsa granda de Kanagawa de Hokusai, vers 1830.
• 
  L'Èrsa de William Thomas Horton, 1898.
• 
  La Novena èrsa d'Ivan Aïvazovski, 1850.