Velocitat

La velocitat (var. abrivada, aviadesa,corsa, rapiditat[1]) es, en fisica, una grandor que mesura lo repòrt d'una evolucion dins lo temps (velocitat de sedimentacion, velocitat d'una reaccion quimica, etc). En cinematica, la velocitat es una grandor vectoriala que mesura, per un movement, lo repòrt de la distància percorrida dins lo temps.
Istòria del concèpte de velocitat[modificar | Modificar lo còdi]

Una definicion formala longtemps manquèt a la nocion de velocitat, perque los matematicians s'enebiguèron de far lo quocient de doas grandors non omogenèas. De devesir una distància per un temps lor apareguèt doncas tan fals coma nos poiriá semblar uèi de far la soma d'aquela doas grandors. Es atal que per saber s'un còrs èra pus velòç qu'un autre, Galileo Galilei (1564-1642) comparava lo repòrt de las distàncias percorridas per aqueles còrs amb lo repòrt dels temps correspondents . Aplicava per aquò l'equivaléncia seguenta:
La nocion de velocitat instantanèa es definida formalament pel primièr còp per Pierre Varignon (1654-1722) lo 5 de julhet de 1698, coma lo repòrt d'una longor infinidament pichona sul temps infinidament pichon mes per percorrir aquela longor. Utilizèt per aquò lo formalisme del calcul diferencial mes al punt catòrze ans pus lèu per Leibniz (1646-1716).
Lo concèpte de velocitat[modificar | Modificar lo còdi]
Cal distinguir dos tipes de velocitat :
- la velocitat mejana, que respond fòrt precisament a la definicion elementària. Se calcula en devesissent la distància percorrida pel temps de correguda ; a un sens sus un periòde donat ;
- la velocitat instantanèa, que s'obten pel passatge al limit de la definicion de la velocitat. Se definís en un instant precís, via la nocion de derivacion . Per exemple dins los calculs de cinematica, la velocitat es un vector obtengut en derivant las coordenadas cartesianas de la posicion a respièch del temps :
Lo vector velocitat[modificar | Modificar lo còdi]
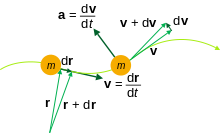
Lo vector velocitat instantanèa d'un objècte que sa posicion al temps es donada per es calculat coma la derivada de a respièch del temps :
L'acceleracion es la derivada de la velocitat a respièch del temps. L'acceleracion es lo taus de cambiament de la velocitat d'un objècte sus un periòde de temps donat. L'acceleracion mejana d'un objècte que sa velocitat passa de a pendent un periòde es donada per :
Lo vector d'acceleracion instantanèa d'un objècte que sa posicion al temps es donada per es :
La velocitat finala d'un objècte aviant amb la velocitat puèi d'acceleracion constanta pendent un temps es:
La velocitat mejana d'un objècte subissent una acceleracion constanta es . Per trobar lo desplaçament d'un tal objècte accelerant pendent lo periòde , remplaçar aquela expression dins la primièra formula per obtenir :
Quand solament la velocitat iniciala de l'objècte es coneguda, se pòt utilizar l'expression :
Aquelas equacions de basa per la velocitat finala e desplaçament se pòdon combinar per formar una equacion qu'es independenta del temps :
Aquelas equacions son validas per la mecanica classica mas pas per la relativitat restrencha. En particular en mecanica classica, totes seràn d'acòrdi sus la valor de e las règlas de transformacion per la posicion creant una situacion ont totes los observators qu'acceleran pas descrivon l'acceleracion d'un objècte amb las meteissas valors. Ni l'un ni l'autre son pas vertadièrs per la relativitat restrencha.
L'energia cinetica d'un objècte se desplaçant en translacion es proporcionala a sa massa e al carrat de sa velocitat :
L'energia cinetica es una quantitat escalara.
Lo cas particular dels coordenadas polaras[modificar | Modificar lo còdi]
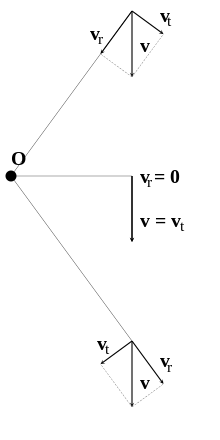
En coordenadas polaras, la velocitat dins lo plan se pòt descompausar en velocitat radiala, , s'alunhant o anant cap a l'origina e la velocitat ortoradiala, dins la direccion perpendiculara (que cal pas confondre amb la compausanta tangenciala), egala a (vejatz velocitat angulara).
Lo moment angular dins lo plan es :
- .
Se reconeis dins
la velocitat areolara.
Se la fòrça es centrala (vejatz movement de fòrça centrala), alara la velocitat areolara es constanta segon la segonda lei de Kepler).
La velocitat en cinematica[modificar | Modificar lo còdi]
Se distinguís :
- La velocitat curvilinèa, qu'es la distància percorrida sus una unitat de temps . Es una grandor escalara.
- Lo vector velocitat o la velocitat dins l'espaci, qu'es lo vector
- ont la nòrma val la velocitat e ont lo sens e la direccion son aqueles del movement de l'objècte considerat. Formalament, lo vector velocitat es la derivada de la posicion de l'objècte a respièch del temps. Quant aquò pòrta pas de confusions, se parla simplament de « velocitat ». E aquí es una grandor vectoriala.
L'unitat internacionala de la velocitat es lo mètre per segonda (m.s-1); pels veïculs coma las automobilas o los avions, s'utiliza subretot lo quilomètre per ora (km/h). Lo sistèma anglosaxon utiliza la mila per ora (mile per hour, mph). Dins la marina, s'utiliza lo nos, que val una mila marina per ora, o 0,5144 m.s-1[2]. En aviacion, se pòt utilizar lo mach, mach 1 essent la velocitat del son (que vària en foncion de la temperatura e de la pression)[3].
Annèxas[modificar | Modificar lo còdi]
Ligams intèrnes[modificar | Modificar lo còdi]
- Acceleracion.
- Acceleracion mejana.
- Cinematica.
- Derivada.
- Dinamica.
- Energia cinetica.
- Fisica.
- Mecanica classica.
- Velocitat de la lutz.
- Velocitat del son.
- Velocitat de fasa.
- Velocitat de grope.
- Velocitat relativa.
- Vector.
- Torsador cinematic.
- Trajectòria.
- Batements per minuta (BPM) : unitat de mesura de la « velocitat » d'un tròç de musica.
Bibliografia[modificar | Modificar lo còdi]
- (fr) Michel Blay, Critique de l’histoire des sciences, CNRS, 2017.
- (fr) Maximilien Marie, Histoire des sciences mathématiques et physiques, Gautier-Villars, 1883.
- (de) Ueli Niederer, « Galileo Galilei und die Entwicklung der Physik », dins Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich, t. 127, n° 3, 1982, pp. 205–229.
- (en) Robert Resnick e Jearl Walker, Fundamentals of Physics, Wiley, 2004.
- (es) Paul A. Tipler, Física para la ciencia y la tecnología, Reverté, 2000.
Nòtas e referéncias[modificar | Modificar lo còdi]
- ↑ Lo Congrès Permanent de la Lenga Occitana, Dicod'Òc, cèrca « vitesse », consultat lo 19 de julhet de 2022, [1].
- ↑ Lo nos es pas plus reconegut per lo BIPM despuei la reforma dau Sistèma Internacional d'Unitats de 2019 (BIPM, Le Système international d'unités (SI), BIPM, 2019, 9a edicion).
- ↑ (de) Jakob Ackeret, « Der Luftwiderstand bei sehr grossen Geschwindigkeiten », Schweizerische Bauzeitung, t. 94, n° 15, 1929, pp. 179-183.






























